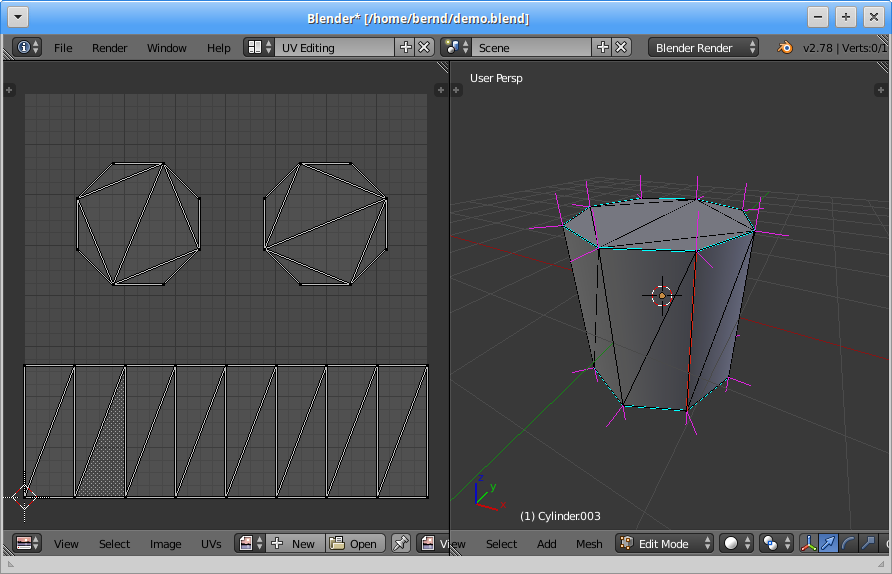
I am trying to export a blender mesh to an OpenGL application.
The problem I am actually fighting with is that of converting the blender representation of a mesh into a representation compatible with the OpenGL drawing model.
Vertices
As the term “vertex” is used in a different notion in OpenGL than in the blender python API, I will try to prevent confusion by using the following terms, when talking about vertices.
I will use the term “blender vertex” for the kind of datastructure represented by type MeshVertex in the blender python API.
I will use the term “trianlge vertex” for a conceptual entity, such that each triangle of a mesh is made up of 3 individual “triangle vertices”.
Thinking the blender python API way, you may identify them with tuples of information available from parallel indexed datastructures such as MeshLoop, MeshUVLoop, MeshLoopColor, sharing the same index.
Naive Approach
Exporters, that I took a look into, simply seem to iterate over the “triangle vertices” stored in, what the blender python API calls “loops”, filling in position data from referenced “blender vertices”.
While this indeed is a working approach, it has the drawback that for the purpose of feeding data to the OpenGL API it may result in a significant memory overhead.
I am not talking about glDrawArrays() that sure needs redundant data like that described before here, but about glDrawElements() allowing reusing the same same tuple of attributes mulitiple times.
Example
To give an example of what I am talking about, will use the following setup.
The scene consists of a triangulated 8-sided cylinder with hard edges between the lateral surface and top and bottom surfaces and soft edges between the individual faces making up the lateral surface.
Naive Approach
This mesh is made up of 16 “blender vertices” with a total of 28 triangles (16 triangles making up the lateral surface and a total of 12 triangles making up top and bottom surfaces).
With each triangle cunsuming 3 “triangle vertices” we come up with a total of 3*28 = 84 “triangle vertices”.
This is exactly the number of elements in each loop layer of the mesh.
Using the before mentioned approach of iterating through the mesh loops, I will end up with a list of 84 entries.
Information Sharing
Taking a second look at the situation it soon turns out, there is lot of redundant information that may be shared between different triangles.
On the top there is a number of 8 “blender vertices” that are used with the same shared attributes (normal, uv) between adjacent triangle lying on the top surface.
The same goes for the bottom surface.
On the lateral surface there is a total of 14 “blender vertices” not lying on the seam that are used with the same shared attributes (normal, uv) between adjacent triangles on the lateral surface.
We will need another 4 entries for the 2 “blender vertices” lying on the seam, to describe the last trianlges of the mesh.
Summing up necessary entries for top, bottom and lateral surfaces we end up with a total of 34 entries, which is less than half of the 84 entries needed using the naive approach.
Right - we will still need another few bytes to store the indices of the entries making up the triangles of the mesh.
Yet we will still get away with less than half of the memory requirement.
2nd Approach
That being said I tried to come up with an algorithm allowing me to cut down the number of required entries to the minimum.
The solution I came up with was hashing tuples of the attributes meeting my requirements to indices into parallel arrays, which seems to work fine.
Yet I still wonder if there might be a better approach.
In case you are fighting on similar problems or might want to review, I posted the relevant snippet of the script below.
def nice_vec(v):return “(%s)” % (“, “.join([”%5.2f” % x for x in v]))
def export_mesh(mesh):bm = bmesh.new()
bm.from_mesh(mesh)
bmesh.ops.triangulate(bm, faces=bm.faces)
bm.to_mesh(mesh)
bm.free()
del bm
mesh.calc_normals_split()
uv_layer = mesh.uv_layers[0].data
position = []
normal = []
uv = []
index = []
attributes = dict()
last_index = 0
for f in mesh.polygons:
[INDENT=2]for loop_index in f.loop_indices:
[/INDENT]
[INDENT=3]loop = mesh.loops[loop_index]
i_vertex = loop.vertex_index
v_normal = loop.normal
v_uv = uv_layer[loop_index].uv
v_normal.freeze()
v_uv.freeze()
l = [i_vertex, v_normal, v_uv]
t = tuple(l)
if not t in attributes:
[/INDENT]
[INDENT=4]attributes[t] = last_index
last_index += 1
v_position = mesh.vertices[i_vertex].co
position.append(v_position)
normal.append(v_normal)
uv.append(v_uv)[/INDENT]
[INDENT=3]
i = attributes[t]
index.append(i)[/INDENT]
# log attributes
n_attribs = len(position)
for i in range(n_attribs):
[INDENT=2]print(“%s %s %s” % ([/INDENT]
[INDENT=3]nice_vec(position[i]), [/INDENT]
[INDENT=3]nice_vec(normal[i]),[/INDENT]
[INDENT=3]nice_vec(uv[i]))[/INDENT]
[INDENT=3])
[/INDENT]
# log indices
print(", ".join([str(x) for x in index]))
# log status report
print("%d (%d)/ %d" % (
[INDENT=2]len(position), [/INDENT]
[INDENT=2]len(index), [/INDENT]
[INDENT=2] len(mesh.loops))
)[/INDENT]