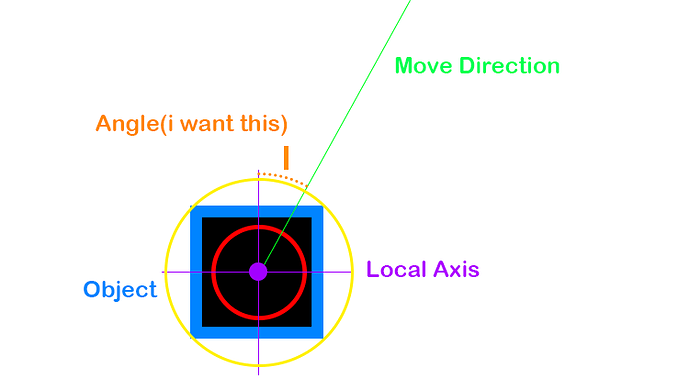
Hello again, I want to make a system where I get an angle, on the “Z” axis, which is obtained from the local direction of movement of the object, but I’m not getting it. I see people using the Numpy module or a “Vector.angle(Vector)” command on the internet, but none of them gave me what I wanted. Can anyone help me?
its dot product. x1x2 + y1y2 + z1z2
I’m a bit of a layman in that, I don’t know what you mean.
(vector1.x * vector2.x) + (vector1.y * vector2.y) + (vector1.z * vector2.z)
parentheses are not necessary i just added them to make it readable.
or better yet. let mathutils do it for you.
https://docs.blender.org/api/blender_python_api_current/mathutils.html?highlight=vector#mathutils.Vector.dot
so vector1.dot(vector2)
order doesnt matter. vector2.dot(vector1) yields same result.
Thanks, one more thing, this first vector, which .dot () is applied, which vector can I apply to that? Since he can’t be zero.
depends on what vector you need, but you can make your own vectors.
vec = [0,0,1] # z vector of 1 unit
the object itself
vec = object.worldPosition.z.copy()
oreintation is also a vector.
Maybe i cant apply it, the result’s so bad, random numbers, i want euler or degrees orientation.
use
ori = obj.worldOrientation.to_euler()
print(ori.x)
or
import math
angle = 45
#radians to degrees
degrees = math.degrees(angle)
#degrees to radians
radians = math.radians(angle)
Everytime I read your replies with code like that, I die a little inside (in a good way). I spent SO MUCH TIME relearning old highschool maths to do that stuff the hard way, and months later I stumble across one of your posts with the whole thing way more easily calculated.
Maybe I should ask more questions in this forum ![]()
orientation? you asked for an angle.
but getting it from dot product then finding the sign for that is a little too much alright. i get it.
if youre only going to rotate on z, [0, 0, degrees(atan2(b.y, b.x) - atan2(a.y, a.x))].
that’d be the classy way around.
i didnt even graduate. id recommend double checking every last formula i share.
This topic has confused me. I’ve canceled replying to it half a dozen times since it started. The OP wants an angle but in relation to what? The direction the object is moving. Okay. How is it moving? By itself? Is it rotating on it’s own and moving in that direction? Will the angle be relative to an orientation local to the object or is it relative to the unchanging world axes?
Get your first vector, whichever one that is considered the the starting vector(0 degrees). If it’s a local vector, convert it to world with
vec1 = object.getAxisVect(vector) # [1,0,0] for X+, [0,1,0] for Y+, [0,0,1] for Z+
Get your second vector, the one that is the movement direction. How you do that is particular to how the thing is moving but whatever it is most likely it will be a vector to begin with. This vector should also be in world coordinates.
Now to get the angle in radians:
rad_angle = vec1.angle(vec2)
and into degrees(don’t forget to import math):
deg_angle = math.degrees(rad_angle)
Am I oversimplifying this? What am I missing? Lots of guesswork makes things more complicated than they should be.
yes, vec1.angle(vec2) is the most effective way of getting angles. i use it all the time. dot product is something else, it doesnt increase linearly in relation to a rotation (45° != 0.5 dot).
oh, woopsie! thats right actually.
arccos( dot(a, b) / (length(a)*length(b)) ) is more like it. looks like i was oversimplifying a little too much there :B
but this still gives us the unsigned angle doesnt it. aaah, mathutils you sexy beast.
Thank’s so much guys, i got it.