First is pretty simple:
The Mesh / Torus Objects / Torus Knot
There are 3 choices:
1 = 3,2 / Trefoil Knot
3 looks like a 4,3 Torus Knot (I could be wrong)
what’s 2 (or if I’m wrong, also, what’s 3)?
Second question.
I’m looking at this:
from this (PDF):
Decorative Knotting Using Trigonometric Parametrizations
http://www.ymmf.hu/sites/talata.istvan.ymmf.hu/files/2014_osz/tergeom_zh_segedanyagok/Decorative_Knotting.pdf
I’m trying to do the Square Knot -
so basically here’s the code:
From This:
x = 0.45*cos(0) + 0.25*cos(-0) - 0.45*cos(-3*0)
y = 0.45*sin(0) + 0.25*sin(-0) - 0.45*sin(-3*0)
z = 0.2*sin(5*0)
to This:
def k3(t):
x = 0.45*math.cos(t) + 0.25*math.cos(-t) - 0.45*math.cos(-3*t)
y = 0.45*math.sin(t) + 0.25*math.sin(-t) - 0.45*math.sin(-3*t)
z = 0.2*math.sin(5*t)
return mathutils.Vector([x,y,z])
modifying the code in:
add_mesh_torus_knot.py
Plugging in my code, I get the following
(which looks close, but, not quite):
What am I doing wrong? How do I bridge the gap?
(Ok, three questions but, two on the same topic)
Thanx
Attachments
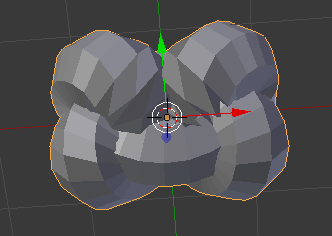
Figured out the second part:
def k3(t):
x = 6*(0.45*math.cos(t) + 0.25*math.cos(-t) - 0.45*math.cos(-3*t))
y = 6*(0.45*math.sin(t) + 0.25*math.sin(-t) - 0.45*math.sin(-3*t))
z = 6*(0.2*math.sin(5*t))
return mathutils.Vector([x,y,z])
(Just had to ratchet up the size):
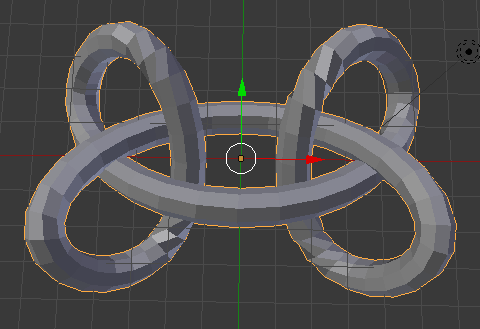
Next question:
(Question 4 - Still related)
In the addon, the knots are setup:
defk1, defk2, defk3
Variables here:
def make_knot(knotidx, ures):
knots = [k1,k2,k3]
and here:
objecttype = bpy.props.IntProperty(name="Knot Type",
description="Type of Knot",
default=1, min=1, max=3)
Rather than just commenting out k1 - k3
and inserting my own code, how would I modify the code
to add k4, k5 etc?
I’ve tried modifying the code in the places I’ve noted, but,
it still doesn’t work. I’m missing something.
Thanx
Assuming you’re talking about the Mesh Extra Objects add-on?
Define your k4 and k5 functions:
# after k1 - k3 functions
def k4(t):
# your code here
def k5(t):
# your code here
Modify the make_knot function:
def make_knot(knotidx, ures):
knots = [k1,k2,k3,k4,k5]
# original code here
Modify property in the AddTorusKnot class:
objecttype = bpy.props.IntProperty(name="Knot Type",
description="Type of Knot",
default=1, min=1, max=5)
And of course, disable/enable the add-on afterwards.
Stan, I could’ve sworn that’s what I did the first time around.
Didn’t work the first time.
Second time’s the charm.
You must’ve reached through the virtual line, caught the code’s
attention and wrangled it into line.
That must be it.
You intimidated my code.
(Yeah, this is what I get for being unemployed and 59 - 3 years away from
early retirement. Employment market being what it is, I’ve got TIME to tinker.
This is just my latest - as you already know, Stan. Feels great to be one of
those senior citizens just CLUELESS about technology  )
)
Thanx.
I can get SOME of the examples working.
Some others, I get glitches:
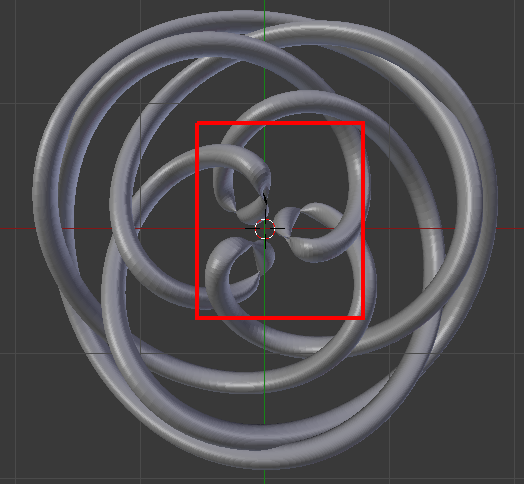
Something like this or
the code just doesn’t mesh
with the execution code
where all the pieces are plugged in.
Ah, well.
Maybe a better programmer than
I (wouldn’t take much at all to be
better than I), might be able to
figure this out.
Still curious as to the knot ID’s for
knots 2 and 3, if anyone knows.
My references for all of this:
(the PDF above)
as well as:
Decorative Knot Patterns
Credit to the Author.
except for glitches as noted
(You’ll also need to modify the code per Stan’s solution
in order to see the additional options in the menu)
def k4(t):
x = 6*(0.45*math.cos(t) + 0.25*math.cos(-t) - 0.45*math.cos(-3*t))
y = 6*(0.45*math.sin(t) + 0.25*math.sin(-t) - 0.45*math.sin(-3*t))
z = 6*(0.2*math.sin(5*t))
return mathutils.Vector([x,y,z])
def k5(t):
x = 6*(0.45*math.cos(t) + 0.25*math.cos(-t) - 0.45*math.cos(-3*t))
y = 6*(0.45*math.sin(t) + 0.25*math.sin(-t) - 0.45*math.sin(-3*t))
z = 6*(0.25*math.sin(4*t) + 0.185*math.sin(2*t))
return mathutils.Vector([x,y,z])
def k6(t):
x = 4.5*(1.5*math.cos(t) + 0.35*math.cos(3*t) - 0.9*math.cos(5*t))
y = 4.5*(math.sin(t) + math.sin(3*t) - 0.9*math.sin(5*t))
z = 4.5*(0.35*math.sin(8*t)-0.2*math.sin(2*t))
return mathutils.Vector([x,y,z])
def k7(t):
x = 4.5*(math.cos(4*t) + 0.875*math.cos(7*t))
y = 4.5*(math.sin(4*t) + 0.875*math.sin(7*t))
z = 4.5*(0.35*math.sin(12*t)-0.15*math.sin(3*t))
return mathutils.Vector([x,y,z])
def k8(t):
x = 4.5*(math.cos(2*t) + 0.67*math.cos(7*t))
y = 4.5*(math.sin(2*t) + 0.67*math.sin(7*t))
z = 4.5*(0.2*math.sin(10*t)-0.1*math.sin(5*t))
return mathutils.Vector([x,y,z])
def k9(t):
x = 4.5*(math.cos(t) + 0.2*math.cos(3*t) + 0.98*math.cos(-5*t))
y = 4.5*(1.875*math.sin(t) + 0.665*math.sin(3*t) + 0.45*math.sin(-5*t))
z = 4.5*(0.35*math.sin(8*t) + 0.15*math.sin(2*t))
return mathutils.Vector([x,y,z])
What doesn’t (as noted above):
def k10(t):
x = 4.5*(0.59*math.cos(t) + 0.3*math.cos(-2*t) - 0.45*math.cos(-5*t))
x = 4.5*(0.59*math.sin(t) + 0.3*math.sin(-2*t) - 0.45*math.sin(-5*t))
z = 4.5*(0.1*math.sin(9*t) + 0.25*math.sin(6*t))
return mathutils.Vector([x,y,z])
def k11(t):
x = 4.5*(0.6*math.cos(t) + 0.25*math.cos(-3*t) - 0.26*math.cos(9*t))
x = 4.5*(0.6*math.sin(t) + 0.25*math.sin(-3*t) - 0.26*math.sin(9*t))
z = 4.5*(0.12*math.sin(16*t) + 0.06*math.sin(4*t))
return mathutils.Vector([x,y,z])
def k12(t):
x = 4.5*(math.cos(2*t) + (1 + 0.45*math.cos(3*t) + 0.4*math.cos(9*t)))
x = 4.5*(math.sin(2*t) + (1 + 0.45*math.cos(3*t) + 0.4*math.cos(9*t)))
z = 4.5*(0.2*math.sin(9*t))
return mathutils.Vector([x,y,z])
def k13(t):
x = 4.5*(math.cos(3*t) * (1 - 0.175*math.cos(2*t) + 0.5*math.cos(8*t)))
x = 4.5*(math.sin(3*t) * (1 - 0.175*math.cos(2*t) + 0.5*math.cos(8*t)))
z = 4.5*(0.15*math.sin(16*t))
return mathutils.Vector([x,y,z])
Feel free to add, take away, improve (or not).
One other not so small glitch I just noticed.
If you pick one knot, move to a different layer
and pick a different knot, it changes your first
knot to the new knot.
You can’t have two different knots in the same
blend from this.
(Solution: Edit mode - P - “By Loose Parts”)



 )
)