Wow this was a really useful lesson! And I took the time to understand it and since I haven’t seen too many clear explanations of these nodes I thought I would share my understanding of how this works.
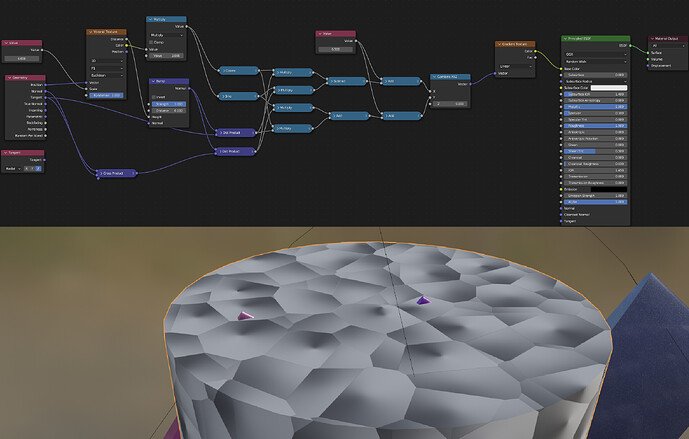
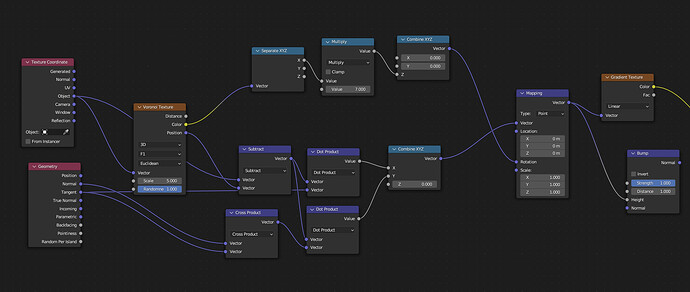
Although quick side note I realised thanks to going through the understanding of the vector maths that using the geometry position vector would affect both the voronoi cells and orientations if I moved the object due to it being linked to the world coordinates. Using the Object Texture Coordinates instead fixes these values to the object itself:
So I hope this explanation helps anyone like me trying to learn procedural methods as well as just revising their vector maths.
Using the object coordinates to drive the voronoi cells means that the cells all take on the same vector equal to the one at the centre of the each voronoi cells.
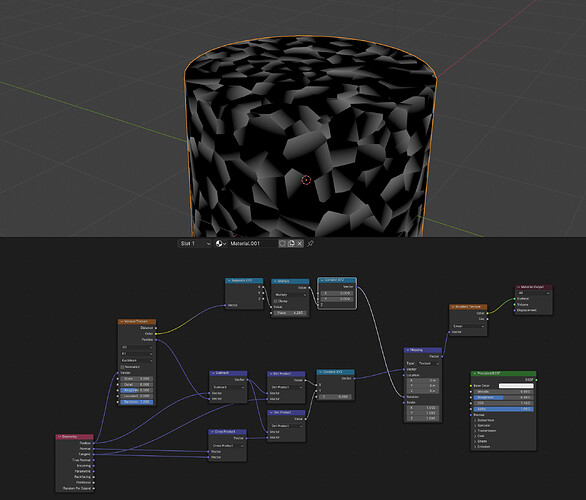
Subtracting the voronoi position vector from the object vector causes each cell to produce vectors that are inward facing towards the centre of each cell.
Taking those resulting vectors and performing a dot product with the geometry tangent vector causes the result to be essentiually a measure of alignment of the inward facing vectors with the tangent vector, thus producing a gradient in the tangent direction of each cell.
Doing the cross product of the normal and tangent geometry vectors creates a bi-tangent vector across each surface which is another tangent vector that is perpendicular to both the tangent and normal vector (hence its name of bi-tangent).
Performing the dot product of this vector with the subtracted voronoi and geometry vector (which produces the field of inward facing vectors towards the centre of the voronoi cell) creates another scalar gradient which is actually perpendicular to the previously created one.
Combining these two as X and Y components with Z=0 creates a field of 2D vectors with X Y values along each voronoi cell. These vectors contain gradient information in both the X and Y directions, essentially capturing how aligned the inward-facing vectors are with both the Tangent and the Bitangent (or the secondary Tangent perpendicular to the first).
Then we use a single RGB channel from the voronoi colour cells to drive a random rotational value in the Z direction through the mapping node to rotate the resulting gradients in random directions.
It was so useful to run through a working example.
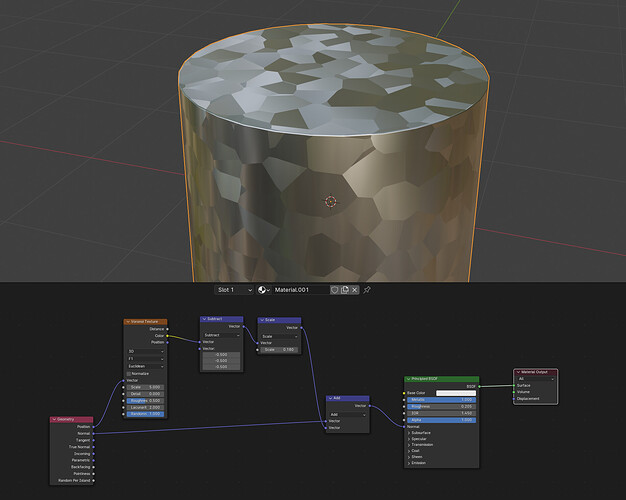
To @LordoftheFleas, What I am trying to do in the end is also add in the ability to vary the intensity of the gradient (so affect the contrast of the bump per cell), as well as the average height of each cell (so brightness) so that the texture can affect the direction of the crystals, slant, and height. So that is what I will work on next. Thank you for the help.
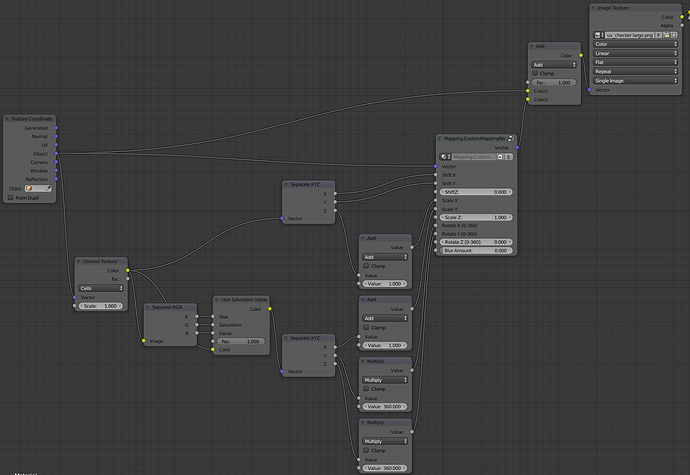
 It’s nice and brilliant, but I can’t wrap my head around what is actually going on. I’ve setup a completely different way, if the idea was to scramble the UVs up based on colored output from voronoi. I’m getting 6 “different” (enough, 3 last ones is just a hsv modifier using the same color output) outputs plugged into a custom mapping node, since the vanilla mapping node doesn’t allow anything to be plugged in. See
It’s nice and brilliant, but I can’t wrap my head around what is actually going on. I’ve setup a completely different way, if the idea was to scramble the UVs up based on colored output from voronoi. I’m getting 6 “different” (enough, 3 last ones is just a hsv modifier using the same color output) outputs plugged into a custom mapping node, since the vanilla mapping node doesn’t allow anything to be plugged in. See