How can I print the coordinates of resolution points of a Bezier Curve?
You probably have to interpolate the spline segments yourself. I tried using a “Follow Path” modifier on an Empty to animate the empty along the curve, but it did not follow the path exactly.
You can access your curve directly and interpolate using the control points defined on the curve.
import bpy
import mathutils
# Assumes your active object is a Bezier Curve.
obj = bpy.context.active_object
curve = obj.data
# Assumes your Bezier is composed of only one spline.
spline = curve.splines[0]
segmentResults = []
# Iterate the control points in the spline and interpolate them.
for i in range(1, len(spline.bezier_points)):
# You always need at least 2 points to interpolate between. Get the first and
# second points for this segment of the spline.
firstPt = spline.bezier_points[i-1]
secondPt = spline.bezier_points[i]
# Get all the points on the curve between these two items. Uses the default of 12 for a "preview" resolution
# on the curve. Note the +1 because the "preview resolution" tells how many segments to use. ie. 2 => 2 segments
# or 3 points. The "interpolate_bezier" functions takes the number of points it should generate.
segmentResults.append(mathutils.geometry.interpolate_bezier(firstPt.co, firstPt.handle_right, secondPt.handle_left, secondPt.co, 12+1))
This will give you a list that contain a list of all the points. You would then need to stitch the results together if you wanted a complete linear list. Note that there will be duplicate points where the last point in a previous segment is also the first point in the next segment. You probably want to filter that out.
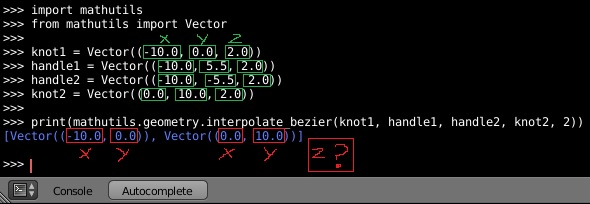
Thank @kastoria for the instructions  . The “mathutils.geometry.interpolate_bezier” almost solved. Unfortunately it generates vectors in two dimensions, X and Y. It ignores the Z dimension :(. So the question still persists.
. The “mathutils.geometry.interpolate_bezier” almost solved. Unfortunately it generates vectors in two dimensions, X and Y. It ignores the Z dimension :(. So the question still persists.
nope, interpolate_bezier returns 3d coordinates, if the input knots and handles are also 3d. Most likely you have Curve type set to 2D and not 3D
bpy.data.curves[0].dimensions
nothing. that should work. it is possible a bug in your version of blender, what version is it? when did you download it?
import bpy
import mathutils
knot1 = -10, 0, 2
handle1 = -10, 5.5, 2
handle2 = -10, -5.5, 2
knot2 = 0, 10, 2
a = mathutils.geometry.interpolate_bezier(knot1, handle1, handle2, knot2, 2)
print(a)
should work, but apparently doesn’t. I’ll have a look at the bug tracker, else submit a report.
version 2.73 (sub 4), branch b’master’, commit date b’2015-01-28’ b’09:36’, hash b’ce52e78’, b’Release’
build date: b’Wed 01/28/2015’, b’10:44 AM’
Weird, on OSX 10.9.5 running Blender 2.71 I get 3D coordinates from that function.
Wooow. This is good news. ![]()
Only I find it strange that despite so many modules to import in Blender python, it remains to calculate the coordinates of the interpolation points of a Bezier curve. And not simply import them.
Kastoria, it was broken only very recently.
mano-wii Yeah, I know what you mean, it would make sense to have such a function as part of the spline data-type. An old StackExchange discussion about this
to make the panel only appear given a restriction, (ie, only an object of type==‘CURVE’ is selected) then you use a poll in your panel class
<b>@classmethod</b>
<b>def</b> poll(cls, context):
<b>return</b> (context.object.type == 'CURVE')
or something. See http://www.blender.org/api/blender_python_api_2_73a_release/bpy.types.Panel.html?highlight=panel%20class
Right!
And not just print, but refer to the value of the u-coordinate
so that that can be used as “factor” in a Cycles node setup. HOW?? :eek:
Someone knows if Is it simple Making a option to cancel the python action? That in the case of calculations are taking a long time. As when you put the Dist = 0.
@mano-wii, i think what you’re referring to is the classic ‘halting-problem’ in computer science. A theorem that suggests that it isn’t possible to tell if a function will go into infinite loop without actually running it to see what it does. This theorem I think may be related to the concept…the theoretical…generic case. not being predictable. The limited case can be somewhat avoided though, Ie, if you know Dist=0 is not a good idea, your code should prevent that Dist value ever being 0. You must put something in between the users input and the code that sets the Dist value. A check … or a min=0.002 as part of the bpy.props.FloatProperty, so the user can’t by accident set that value
@zeffii I tested with the Dist = 0 and realized that really is not a good idea. Hahaha XD.
So I limited a min=0.01.
But I’d really like was able to cancel the calculations.
But that’s not really necessary.
Thank U