i want to make an animation of a cross section of a hypercube appearing and disappearing as it passes through the 3d plane, how to do this in blender?
I’d compute the vertices of the intersection of the 4D Hypercube with the 3D space, depending of the position and rotation of the 4D cube. Then I’d use the convex hull node geometry node to compute a mesh from it.
I don’t know a good algorithm for computing the intersection vertices, though, and also have no experience with the convex hull node (Blender version 3.0).
So, without any formal or reviewed proof, I am still pretty sure that you can compute the vertices of the intersection by checking each edge of the hypercube for intersection with 3D space (not all edges intersect). Then compute the convex hull of all those vertices resulting from edges intersecting 3D space.
A tesseract has 32 edges, so it should be manageable to do this in geometry nodes.
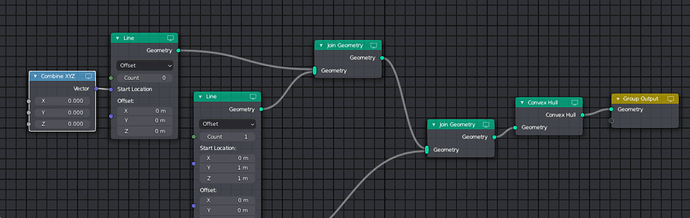
I’d check, for each edge, whether it intersects and control the properties of a line node with the results. IN particular, use offset [0,0,0] and count = 1 if there is an intersection and count = 0 if there is none. Then feed all the lines into join geometry nodes and the last output into convex hull.
For the 4-Dimensional vectors of the hypercube you probably have to add additional attributes and do the matrix transforms and vector translations manually.
I’m a little confused, first how could I make the hypercube shape in the blender? and how would i generate the shape of the cross section of it?
and that of course… would be a cube the generated shape. Is there a way to do what I want using the Boolean modifier? this video is an example of what I want to do https://youtu.be/E4yESsoHtjo
You could create the resulting shape by using Booleans, but then you would have to calculate the shape and positions of the intersecting shapes. I guess you will not get around doing some mathematics to calculate the shape of the intersection before you can visualize them in Blender. If there is a trick to use Blender’s internal 3D system to do 4D computations, I don’t know it, which is why I’d resort to code the computations myself (e.g. using geometry nodes).