Posted this in Asking for Tutorials thread:
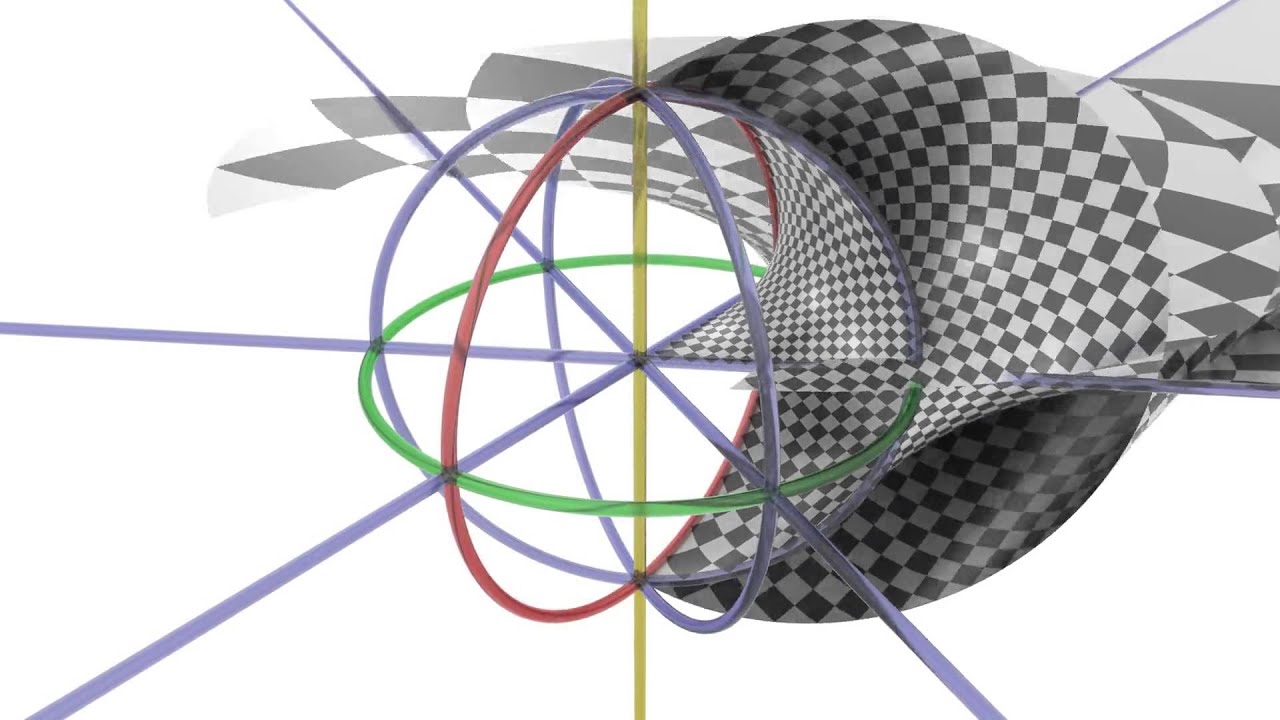
Lawson’s minimal surface (or something comparable):
https://imaginary.org/hands-on/lawso…ace-of-genus-2
It appears to have non-symmetrical edges. They seem to
converge at the center and widen out the further away from
the center they get.
It also looks as though the edges thicken the further away
from center they get.
I’ve seen this described elsewhere as a sort of logarithmic
grid.
I’m no math wizard, so, I could be wrong on any/all of this.
Blender seems to do (subdivide) symmetrical, but not non or
asymmetrical (that I’ve noticed).
I could be wrong on that too, I’m no blender whiz.
I’ve looked at attempting to subdivide a plane and then roll it
up into a donut, but, with symmetrical edges and no way, that
I’m aware of to adjust the edges as shown in the above linked
example, I could just as easily use the mesh Torus Knot.
Is there a way to do this using a Math Function xyz preset?
Would this be more easily done using a python script?
Or perhaps using the Sverchok addon and a script node?
Or what?
I don’t understand the formula for Lawson’s minimal surface, even if I did,
I have no idea how to port it over to a python script or a Math Function xyz
preset or if it’s even possible.
I have used: MathMod, TopMod, K3DSurf (all of which can export to Mesh) and looked at the program referred to in the link “Surfer” (under “Programs”)but, there’s no examples on this.
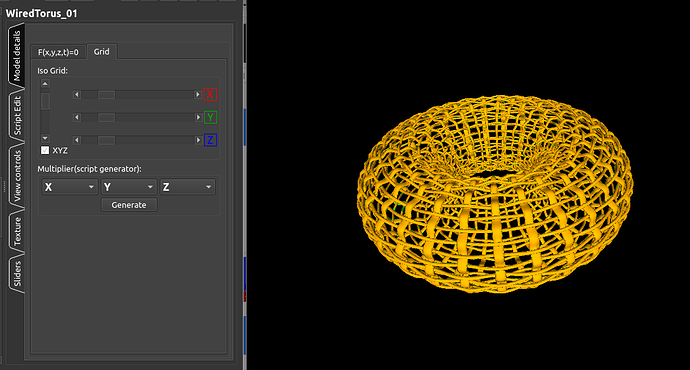
Under MathMode IsoSurfaces, there is a similar example: “Wired Torus”, but it’s woven:
Thanx