The other day I wondered if I could simulate a parabolic reflector by enabling deflection and dropping particles to see if they cross the focal point. The results were very accurate.
Wow! That is cool!
Any possible hope of you sharing the .blend?
Edit: My only crit is the lighting. It would look better with just one light, no shadows, AO, and keep the specular the same.
Thanks!
Here’s the .blend as requested. I deleted my original lighting setup and added a plain lamp. Let me know if anyone is interested in the technique I used for modeling a parabola.
I sure am interested. I’ve tried before. Thanks for the .blend!
Let me know if something I wrote is unclear.
I’m not entirely sure you wrote the tutorial right, but I understand what you’re saying. Thanks!
an easier way is to just add a uv-sphere from top view and scale it on the z axis. then you just delete the top half of the sphere and you have a parabolic bowl. to change the focal point, just scale it more.
Attachments
Sure, your way is easier, but mine is more complicated. ![]()
Actually, I didn’t know that scaling a sphere along an axis would give you a true parabola. How did you learn that?
scaling a sphere would not make a parabola. the slicing technique is more accurate, though technically, it is a half-ellipse. to get a true parabolic slice, your slicing plane would need to be parallel to the side of the cone. hm, my math teacher was right, someday i would use that…
it would be nice if blender could make a curve of a specific function
Technically speaking though, it’s not a parabola, but a paraboloid of revolution 
Thanks for the clarification.
You guys rock!!
http://en.wikipedia.org/wiki/Paraboloid
http://en.wikipedia.org/wiki/Conic_section
Heh, I have that from Wiki as well, as I’d once edited that page (the Dutch version though) and remembered it from there. The conic section is great!
hmm, looks like i need to brush up on my math a bit. Mexicoxican is right, mine is not a true parabola, but it does look similar to one. useful for faking parabolas, but Dbugged’s way is accurate.
This seems interesting though when i spin my “half-circle” it gets screwed. I guess an image says more than anything else!
See my attachment.
Attachments
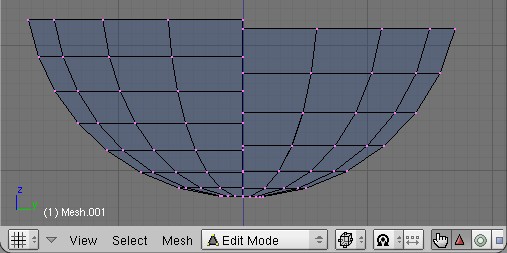
:eek: How did you do that?
Make sure before you delete half the vertices, you center new and snap the cursor to selection. When you spin make sure all verts are selected and you are in top view.
Dbugged’s way is not entirely accurate; he made an elipse, not a true parabola.
Try making your own cone using the spin tool on one vert, and extruding all the edges in. Then delete doubles and move the center vert up. Try to make the edge a perfect 45° angle by using the snap to grid feature. Then use a plane and the knife script with the plane rotated 45 degrees and put in the cone. I made a perfect parabola that way. If only i could find my thumb drive so I could show you…
According to the wikipedia, a true parabola can be achieved using the same method I used to get an ellipse. The only difference would be that the slice should be parallel to the side of the cone, as mexicoxican said.
Yes, and that’s what I did. I made my own cone using spin and snap to grid, (and extrude) and made the side 45° to the base of the cone. Then I used a plane to slice it at 45°. Then I rotated it 45 degrees to make it so I could spin it into a bowl.
Perfect parabola.
So, drifting a bit from the subject of blender tests, what is the practical difference between a parabola, ellipse, and hyperbola? What I originally created was an ellipse, but it still focused the particles to a point. I know that a parabola will reflect any particle it captures through the focal point as long as the particles travel along the axis perpendicular to the parabola (in this case, the z-axis).
Do ellipses and hyperbolas not do the same thing? Apperently not, otherwise they would have the same curve as a parabola.
Please forgive my limited education. I only graduated high school. :o