Hello,
it seems that I don’t understand the locale coordinate system.
I try to simulate a kelvin wake with particles.
The first problem is that the particle’s location attribute uses the global coordinate system.
So if the moving emitter follows a curve the particles do not turns with him.
I tried to solve the problem by converting the modified particles position into the emitter’s locale position:
mat_inv = object.matrix_world.inverted() #object is the emitter
#Formulars are taken from "A VFX ocen toolkit with realtime preview " by Björn Rydahl page 16
#https://www.diva-portal.org/smash/record.jsf?pid=diva2%3A272268&dswid=1yVqr7fD
xp = old_xp+ (-phase * (2 * math.cos(t) - math.pow(math.sin(t),3)))
yp = old_yp + (-phase * (math.cos(t) * math.pow(math.sin(t),2) ))
zp = old_zp
# converting the particle's global coordinates to local coordinates
mat_loc = mathutils.Matrix.Translation((xp,yp , zp))
mat_loc = mat_inv @ mat_loc
#getting the vectors for location , rotation and scale from matrix. Rotation and scale are not used
locale_location, rot,sca = mat_loc.decompose()
First question:
Is this the correct way ? Or are there any logical errors ?
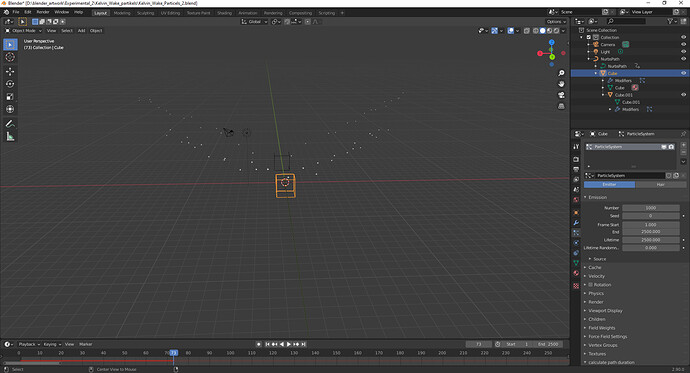
If I don’t convert the particles into locale coordination system I get this:
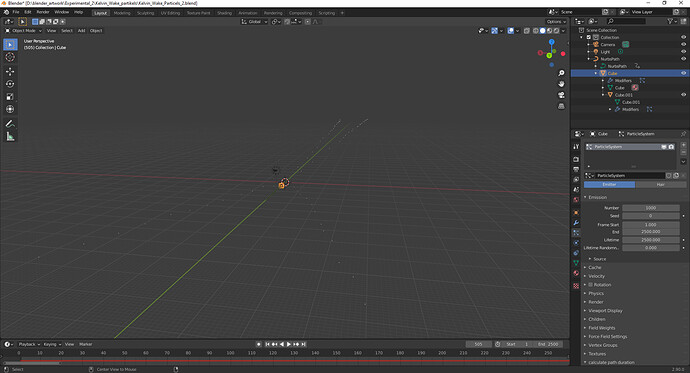
If I convert the coordinates into the local system I get this:
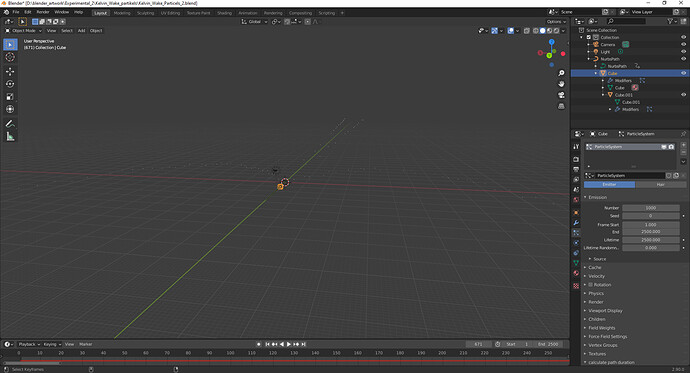
later in frame 671:
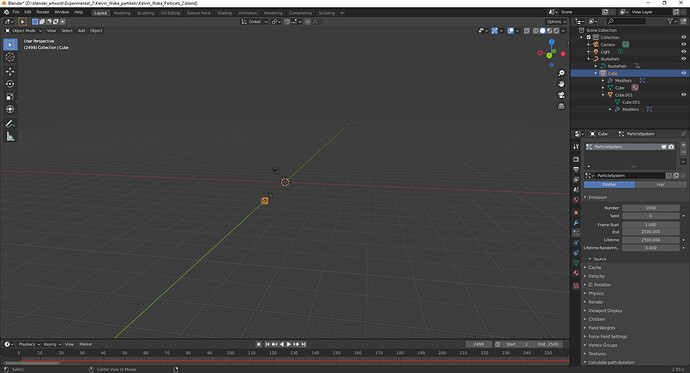
end at last in frame 2498 out of 2500
If I move the emitters along the global y-axis and start the animation from I get this:
The particle flow is constant during the whole animation but the particle-curve is smaller like this in the first picture with global coordinates. All particle-curves has the same parameters (phase,t).
I expected that the flow behaves like in the first picture. Can me someone explaine why it doesn’t work this way after converting the particles global coordinates in locale coordinates ?