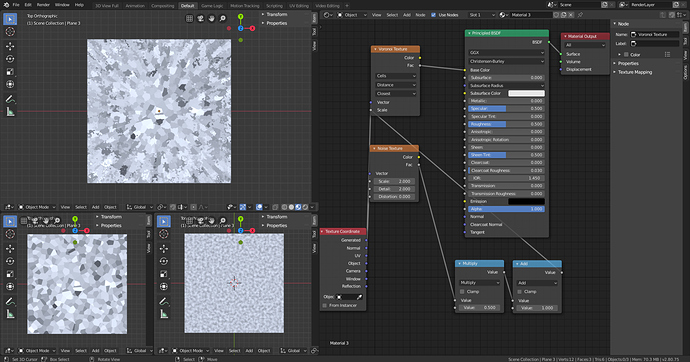
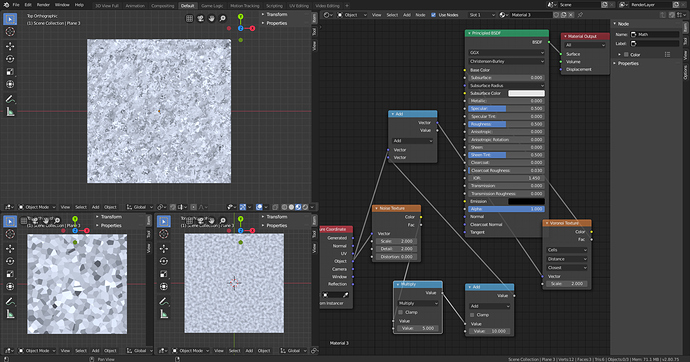
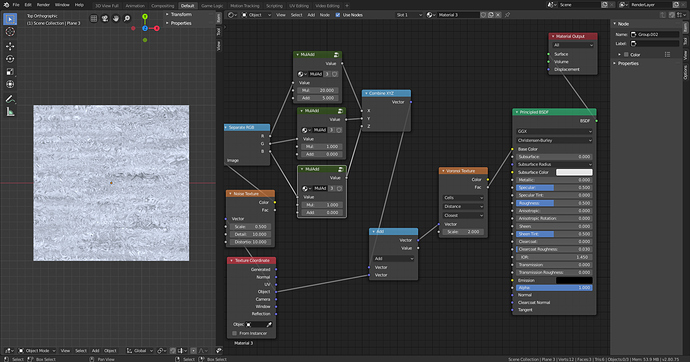
I believe the above image explains my dilemma. I have two uniform textures that I combine, and somehow end up with a texture that depends on location. I would like to have some insight on why this occurs.
You connected the noise output to the scale input of the voronoi. Scale is basically a premultiplier for the coordinate vector. So the larger the coordinate the larger the effect.
If you tell me what kind of texture you actualy want to get, I might be able to tell you how to do it. I assume you had something quite different in mind.
How so? When I put in a regular number, my texture is uniform.
Yes, hmm, not sure how I should explain.
If you scale an image and put it on top of the original, at the coordinate origin they will be aligned. The further away you get from the origin, the larger the distance between the same feature on the different images.
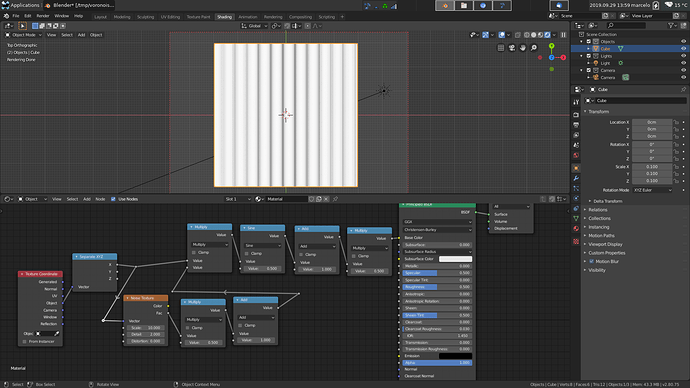
About the latest image, yes, adding the noise is the right way to distort a texture. It might be noticably not isotropic, though, as the add/multiply nodes at the bottom work on scalars, so the displacement will happen only along the space diagonal. To correct that, replace the add/multiply nodes with a vector mapping node.
Yes, that works, too. Seems you figured out the matter.
Let’s try to reproduce this with a simpler texture. Voronoi is complicated to understand, so let’s use a simple sine instead.
Similar to your picture, we get more noise the further away we go from the (0,0,0) point. Why?
Without noise, we are just computing sin(x). With noise, we have sin(x*n(x)), where n(x) is the noise texture. Since sine is a “smooth” function, its output is similar if the input is similar.
What’s the difference between the inputs in both cases? It is given by x - x*n(x) = x(1 - n(x)). The range of 1 - n(x) and n(x) is the same: between 0 and 1. What we get in the end is that sin(x) and sin(x*n(x)) are very similar (that is, the difference between the inputs is very close to zero) when x is close to zero. As x goes further away from the origin, this difference gets larger, and the impact of noise is stronger.
The voronoi texture is quite different from a sine, but it is also smooth. That’s why you get this effect. If you want an homogenous noise, you should, as you’ve already noted, add the noise instead of multiplying it.