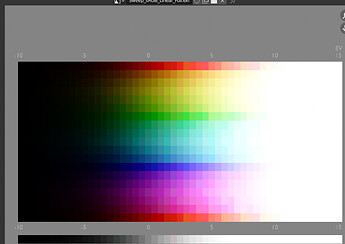
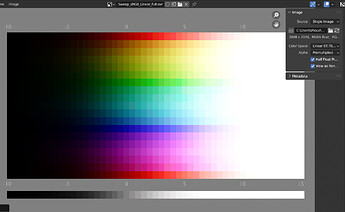
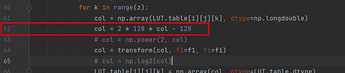
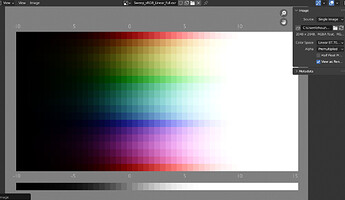
I think I see the issue. Hold on. The domain variables didn’t actually change the internals of the LUT, so I’m going for a completely wrong range.
How about this?
import colour
import numpy as np
def subtract_mean(col):
mean = np.mean(col)
return col - mean, mean
def add_mean(col, mean):
return col + mean
def cart_to_sph(col):
r = np.linalg.norm(col)
phi = np.arctan2(col[1], col[0])
rho = np.hypot(col[0], col[1])
theta = np.arctan2(rho, col[2])
return np.array([r, phi, theta])
def sph_to_cart(col):
r = col[0]
phic = np.cos(col[1])
phis = np.sin(col[1])
thetac = np.cos(col[2])
thetas = np.sin(col[2])
x = r * phic * thetas
y = r * phis * thetas
z = r * thetac
return np.array([x, y, z])
def compress(val, f1, fi):
fiinv = 1 - fi
return val * fi/(1 - fiinv * np.power(((f1*fiinv)/(f1-fi)), -val))
def transform(col, f1, fi):
col, mean = subtract_mean(col)
col = cart_to_sph(col)
col[0] = compress(col[0], f1=f1, fi=fi)
col = sph_to_cart(col)
return add_mean(col, mean)
def main():
f1 = 0.9
fi = 0.8
LUT = colour.LUT3D(name='Spherical Saturation Compression')
LUT.domain = ([[-12.473931188, -12.473931188, -12.473931188], [ 12.473931188, 12.473931188, 12.473931188]])
LUT.comments = [f'Spherically compress saturation by a gentle curve such that very high saturation values are reduced by {((1-fi)*100):.1f}%',
f'At a spherical saturation of 1.0, the compression is {((1-f1)*100):.1f}%']
x, y, z, _ = LUT.table.shape
for i in range(x):
for j in range(y):
for k in range(z):
col = np.array(LUT.table[i][j][k], dtype=np.longdouble)
col = 2 * 12.473931188 * col - 12.473931188
col = np.power(2, col)
col = transform(col, f1=f1, fi=fi)
col = np.log2(col)
LUT.table[i][j][k] = np.array(col, dtype=LUT.table.dtype)
colour.write_LUT(LUT, "Saturation_Compression.cube")
print(LUT.table)
print(LUT)
if __name__ == '__main__':
try:
main()
except KeyboardInterrupt:
pass
Saturation_Compression.cube (1.1 MB)
If this works, I think we need to discuss the relevant resolution. Right now this is a resolution of 33×33×33, which may be excessive or it may be too low. It should be easy to change but I’m not sure what an appropriate scale might be. It’s like 1.1MB as is, and it quickly grows as the size grows. I’m not sure what an appropriate LUT size budget might be.